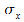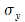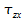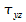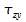Einleitung
Den Begriff "Vergleichsspannung" hat jeder Ingenieur schon einmal gehört. Die meisten werden sich auch noch an die folgende einfache Formel erinnern:
Formel 1
Dabei handelt es sich um die Von-Mises-Vergleichsspannung für Stäbe. Hier sollen aber keine Stäbe mit ihrem einachsigen Spannungszustand betrachtet werden sondern Flächen, die einen zweiachsigen Spannungszustand haben. Wenn nur ein einachsiger Spannungszustand betrachtet werden soll, dann brauchen in den Formeln nur einige spannungen zu Null gesetzt werden. Auf den allgemeinen Spannungszustand wird hier nicht eingegangen.
Begriffserklärung
Zunächst soll erst einmal geklärt werden, was eine Vergleichsspannung ist und wozu man diese braucht.
Der allgemeine Spannungszustand eines Körpers wird durch folgende Spannungen beschrieben:
Diese können als Spannungstensor geschrieben werden:
Formel 2
Beim ebenen Spannungszustand wird es etwas übersichtlicher. Einiger Spannungen werden Null und es ergibt sich folgender Spannungstensor:
Formel 3
Das ist zwar etwas einfacher als in Formel 1 aber immer noch sehr unhandlich.
Die Materialeigenschaften von vielen Materialien werden durch den Zugversuch ermittelt. Neben den E-Modul wird auch eine Zugfestigkeit ermittelt. Mit dieser Zugfestigkeit muss der reale Spannungszustand verglichen werden. Genau dazu dient die Vergleichsspannung. Der reale mehrachsige Spannungszustand wird durch eine einzige Spannung repräsentiert, die im Material die gleiche Anstrengung verursacht wie der mehrachsige Spannungszustand. Dafür gibt es die verschiedensten Annahmen, die Vergleichsspannungshypothesen genannt werden.
Gestaltänderungshypothese (GEH)
Diese Vergleichsspannungshypothese ist auch unter folgenden Namen bekannt:
- Vergleichsspannung nach von Mises
- Gestaltänderungsenergiehypothese
Formel 4
Bei dieser Hypothese wird davon ausgegangen, dass der Werkstoff versagt, wenn die Gestaltänderungsenergie eine bestimmte Grenze überschreitet. Unter Gestaltänderungsenergie wird die Energie verstanden, die eine Verzerrung oder Deformation des Körpers hervorruft.
Bei hydrostatischen Spannungszuständen ist diese Vergleichsspannung Null. Hydrostatisch bedeutet, dass die Spannung in allen Richtungen gleich ist. Wenn näherungsweise ein hydrostatischer Spannungszustand vorliegt, dann sollte diese Hypothese nicht angewendet werden.
Die Vergleichsspannung nach der Gestaltänderungshypothese ist mit Sicherheit die bekannteste und am häufigsten angewendete Vergleichsspannung. Für alle Materialien, die nicht spröde sind, kann diese Hypothese angewendet werden. Ein wichtiges Anwendungsgebiet ist der Stahlhochbau.
Schubspannungshypothese (SH)
Diese Vergleichsspannungshypothese ist auch unter folgenden Namen bekannt:
- Vergleichsspannung nach Tresca
Formel 5
Bei dieser Hypothese wird davon ausgegangen, dass das Versagen durch die maximale Schubspannung hervorgerufen wird.
Besonders im Maschinenbau wird diese Hypothese gerne angewendet. Sie eignet sich besonders für spröde Werkstoffe.
Normalspannungshypothese (NH)
Diese Vergleichsspannungshypothese ist auch unter folgenden Namen bekannt:
Formel 6
Bei dieser Hypothese wird davon ausgegangen, dass die größte Hauptspannung zum Versagen führt.
Mit der Formel werden also nichts weiter als die Hauptspannungen berechnet. Die Hauptspannungen sind per Definition die Eigenwerte des Spannungstensors. Wenn man den Eigenwert des Spannungstensors (Formel 3) berechnet, dann bekommt man genau diese Gleichung (siehe [2]).
Hauptdehnungshypothese (DH)
Diese Vergleichsspannungshypothese ist auch unter folgenden Namen bekannt:
Formel 7
Es wird davon ausgegangen, dass die maximale Dehnung zum Versagen führt. Deswegen kann die Formel auch so ausgedrückt werden:
Formel 8
Literatur
[1] Petersen, Stahlbau, Grundlagen der Berechnung und baulichen Ausbildung, 3. Auflage,Vieweg&Sohn Verlagsgesellschaft mbH, Braunschweig/Wiesbaden
